Am Vormittag des 15. März 2007 findet wieder der internationale Wettbewerb "Känguru der Mathematik" statt, an dem im letzten Jahr über 3 Millionen Schüler von der 3. Klasse der Grundschule bis zur Maturaklasse teigenommen haben. Unsere Schule nimmt daran nur mit den zweiten und dritten Klassen teil. Bisher haben sich 54 Schüler und Schülerinnen gemeldet. Einige davon dürfen im zweiten Semester an einem Vorbereitungskurs (Wahlpflichtfach ab Anfang Februar) teilnehmen.
Die gestellten Fragen (30 Multiple-Choice-Fragen sind in 75 Min. zu lösen) sind ziemlich schwierig, es handelt sich dabei nie um 08/15-Fragen: die Schüler müssen die Texte sehr exakt lesen können und sie müssen die gestellten Fragen verstehen können, was die größte Schwierigkeiten bereiten wird, weil sie sehr selbstständig sein müssen. Die Lösungswege sind grundverschieden, sie verlangen den Schülern alles ab.
Beispiele für gestellte Fragen:
Nr. 8 (leichte Frage = drei Punkte)
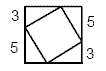
Einem großen Quadrat wird ein kleines Quadrat, wie in der Skizze zu sehen, eingeschrieben. Wie groß ist die Fläche des kleinen Quadrates?
A) 16 B) 28 C) 34 D) 36 E) 49 |
 |
Nr. 14 (mittelschwere Frage = vier Punkte)
Auf einer Geraden g sind vier Punkte und auf einer dazu parallelen Geraden h zwei Punkte markiert. Wie viele verschiedene Dreiecke gibt es, die jeweils drei dieser Punkte als Ecken besitzen?
A) 6 B) 8 C)12 D) 16 E) 18
Nr. 24 (schwierige Frage = 5 Punkte)
Ein Spaziergänger unternahm eine 2-stündige Tour, die sich in folgende Abschnitte unterteilen lässt: in einen flachen Abschnitt, einen ansteigenden und den gleichen Rückweg mit den nun fallenden und dann den wieder flachen Abschnitt. Der Spaziergänger geht im Flachen mit einer Geschwindigkeit von 4 km/h, bergauf mit 3 km/h und bergab mit 6 km/h. Wie lang ist diese Tour?
A) Man kann es nicht wissen. B) 6 km C) 7,5 km D) 8 km E) 10 km
Die Ergebnisse, weitere Statistiken (intenationale Ranglisten), sowie die Fragen und Antworten der Wettbewerbe der letzten Jahre (auch für die Grund- und Oberschule) finden Sie unter:
www.kaenguru.at
Zu den Ergebnissen des Wettbewerbs
